Saturday, May 31, 2008
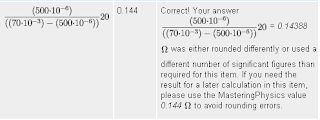
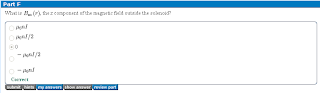
MP9-2: Ampère’s Law Explained
One of the main things to keep in mind here is that it's the symmetry of the closed path you're integrating along that matters, not the amount / consistency of current passing through.
Symmetry lets you bring B out of the integral.
Symmetry lets you bring B out of the integral.
Friday, May 30, 2008
Thursday, May 29, 2008
Tuesday, May 27, 2008
MP9-1: Direction of magnetic field due to a wire conceptual question (spoiler)
Part D: B is 'out of the page' in case you can't read it.
Saturday, May 24, 2008
MP8-2: Problem 31.55 (spoiler)
The answer to this problem is the average of the two voltages; for example, if the two voltages are 2.70V and 1.90V as they were in mine, then the answer is 2.30V. I think Nick had the version where the voltages were 2.30V and 1.10V, so his answer was 1.70V.
I can explain this later if you like; basically since there are two resistors in series of the same amount, the current is the same so the voltage drop must be the same. So, the voltage will drop by half the difference at the point being measured.
I can explain this later if you like; basically since there are two resistors in series of the same amount, the current is the same so the voltage drop must be the same. So, the voltage will drop by half the difference at the point being measured.
MP8-2: Problem 31.65
This one just needs a simple application of both Kirchhoff's loop law and junction law.
The first thing I did was figure out an equation for R_eq (R_ef) for the circuit using what we know about parallel resistors.
Using the junction law, you can easily find the current through the resistor by subtracting the ammeter's max from the current going into the circuit.
Then use the loop law to set V_A = V_R (V=IR) and solve for R_R.
Plugging that into your R_ef gives you a surprisingly pretty number if you use 2nd+ANS (for the full, non-rounded value) on your TI calculator. Or at least for these values, it did.
MP8-2: Problem 31.72
On page 986 of the text, you'll find the equation for the charge on a capacitor in an RC circuit as a function of time: Q = Q_0 * e^(-t/RC)
To figure out what time you'll have x% of Q_0, just set e^(-t/RC) to .x and solve for t.
The key to the second half is realizing that you'll have 1/sqrt(2) (about 70%) of Q_0 when the U_C is halved--
U_C = Q^2 / 2C
U_C /2 = (Q/sqrt(2))^2 / 2C
(page 952)
MP8-2: Problem 31.73
I used an equation that came up during the previous section: V = V_0 * e^(-t/RC)
Solve for R and input data from the point on the graph where t=2ms (2*10^-3).
Wednesday, May 21, 2008
Monday, May 19, 2008
Saturday, May 17, 2008
Monday, May 12, 2008
Thursday, May 8, 2008
Subscribe to:
Posts (Atom)