MP10-2: Reflection and Refraction ranking task (hints)

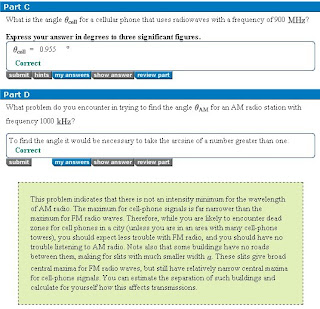
Hint #1: This is a silly problem.
Hint #2: More than 1 card can go in a 'slot'.

MP10-2: Locate the object (practice, spoiler)

MP10-2: A Sparkling Diamond II (practice / spoiler)

The key to Part B is drawing a good diagram and realizing that (theta b) = (alpha) - (theta c).

MP10-2: Refraction through glass and water (spoiler)

Problem Statement:

Answer:

MP10-2: Light refracted through a prism (spoiler)

Problem Statement

Part A

Part B

MP10-2: Sparking Diamond I (spoiler)

MP10-2: Is Light Reflected or Refracted? (spoiler)

MP10-1: Underwater optics (spoiler)

MP10-1: How deep is the goldfish (spoiler)

MP10-1: Resolving pixels on the computer screen (spoiler)

For part A, convert to millimeters as you go with each unit. Use the special formula from the hints for a circular aperture.

For part B, convert to meters as you go.

MP10-1: Understanding the propogation of light (spoiler)

MP10-1: Geometry and reflections (spoiler)

MP10-1: Diffuse Reflection (spoiler)

MP9: Double slit 2 (spoiler)

Use (2 lambda) for the path difference for the second maximum, and (3.5 lambda) for the path difference for the 4th minimum.

MP9: Doorway Diffraction (spoiler)

This is a straightforward plug and chug using the diffraction formula asin (theta) = m * lambda. We are trying to find the 1st minimum so m = 1.

You will find the formula (wavelength) * (frequency) = (wave speed) formula useful here.

MP9: Resolving Power of the Eye (spoiler)

Use the hints; this is a straightforward plug and chug.

Happy Thanksgiving to all in Phys 203 (and others)

Hi, I hope all of you have a nice Thanksgiving! - David

MP9: Problem 22.36 (solution with explanation)

Recall that the intensity is proportional to E^2 where E is the electric field. So, if you have only one half the number of slits, you have one fourth the intensity. 'Nuff said. Peace out.

MP9: Problem 22.18 (solution with explanation)

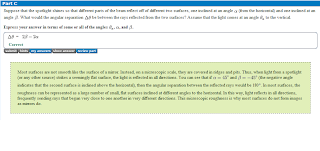
The key to this problem is the basic diffraction relationship asin (theta) = lambda, where lambda is ( the speed of light 3 * 10^ 8 m/s / the given 800 Mhz Frequency), then you multiply by 180/pi to convert to radians.

However, this gives you only half the angle you need. Recall that for diffraction the 1st minima correspond with m=+/- 1, and the central maximum is everything in between. So you need to multiple the above function by 2.

MP8-2: Lights of different wavelengths on a diffraction grating (spoiler - read hints first)

MP8-2: Lights of different wavelengths on a diffraction grating (hints - read this first)

Use the given slit density of the diffraction grating to determine the value of d (specifically, the value of d is the reciprocal of this slit density, but you must convert to meters first).

MP8-2: Double slit 1

MP8-2: Why you can receive AM radio in a city (spoiler)

MP8-2: Using a Michelson Interferometer (spoiler)

This is a plug and chug problem. The hints tell you what to do. For Part A, use the relationship 2y=m*lambda and solve for lambda. For Part B, find the ratio of the measured mirror movement distances, and this will tell you the index of refraction.

MP8-2: Single slit diffraction (spoiler)

I found it helpful to convert to micrometers for each individual measurement. Note the "0.5" in the denominator. I need this because the distance to the central point is only half the distance given of 17.9mm. The "3" in the numerator represents m=3 for the third minimum.

For Part B, recall the equation for refraction m1*lambda1=m2*lambda2. Since water has a higher index of refraction than air, the wavelength will become shorter in water as compared with the original. Since the width of the fringes is proportional to lambda, this will make them narrower.

MP8-2 Overlapping Diffraction Patterns (spoiler - see hint first)

MP8-2 Overlapping Diffraction Patterns (hints)

These hints apply to Part C

MP8-1: Fringes from different interfering wavelengths (spoiler with explanation)

Hints for this problem: Start with the constructive interference equation, use the small angle approximation (sin x = x) and solve for theta when m=1 (it isn't m=0 because that would be for theta=0 and we know there is an nonzero angle based on the problem description).

The theta will be the same for the destructive scenario, since the destructive band with the second wavelength occurs in the same place as the constructive band for the original wavelength. Use m=0, since this is the first destructive interference band.

Solving this relationship shows you that the second wavelength is twice the first, which you then convert to micrometers.

Problem 22.4

Print ViewFringes from Different Interfering Wavelengths

MP8-1: "understanding" Fraunhofer Diffraction

For Part C, strange that m=0 is excluded. I will ask Francois to go over this on Wed.


For the last part, notice that I convert everything explicitly to millimeters.

MP8-1: Problem 22.4 (spoiler)

For this problem use the so-called "small angle approximation" or sin x = tan x = x. So you can replace sin (theta) with just theta in the interference equation, and solve for d, the spacing between the two slits.

I converted all the units to meters initially, and the final 10^3 power is to convert from meters to millimeters.